[Bayes] Bayesian inference(베이즈 추론)의 배경

 

베이즈 추론이란?

 

 

(블로그가 지루하다는 친구의 피드백을 받아 물음표 이모티콘 넣어드렸습니다ㅎ헿)

베이즈 추론은 토마스 베이즈와 라플라스가 18세기에 창시한 것으로 통계학의 베이즈 확률론을 기반으로 한 통계적 추론이다. 추론할 대상의 확률 분포를 추정하는 것이 목적이며 확률은 다양한 이벤트와 지식을 바탕으로 주관적인 정도로 해석해 업데이트 한다.

 

 

확률

 

1. 함수

𝑃 ∶ ℬ → [0, 1]

• 𝓧 : 집합
• ℬ : 𝓧의 부분집합들의 모임

𝑃는 𝓧의 부분집합들의 모임에서 0으로 가는 함수다.

아래의 세가지 성질을 만족해야 한다.

(i) 𝑃(𝐵) ≥ 0, ∀𝐵 ∈ ℬ;

    💡 함수값은 항상 0보다 크거나 같다.

(ii) 𝑃(𝓧) = 1;

    💡 전체집합에서 확률값은 1이다.

(iii) (가산 가법성) ℬ의 부분 집합으로 이루진 집합들의 열 (𝐵𝑛)이 서로소다

    💡 서로소는 집합끼리 겹치는 것이 없다는 뜻이며 가산 가법성이 만족해야 한다.

 

각각의 합집합의 확률은 각각의 확률을 더한것과 같다는 식이 도출되고 세가지 성질을 만족하는 것을 확률이라고 한다.

스크립트 𝓧를 표본공간이라고 하고 (𝓧,ℬ, 𝑃)가 정의된 것을 확률 공간(probability space) 이라고 한다.

또한 스크립트 ℬ의 원소(𝓧의 부분 집합)를 사건(event)라고 한다.

어떤 집합 𝓧상에 정의된 확률 𝑃는 𝓧의 모든 부분 집합에 0과 1 사이의 값을 대응시킨 다음의 조건들을 만족하는 함수다.

 

2. 조건부 확률

𝐴, 𝐵 ⊂ 𝓧이고 𝑃 𝐵 > 0인 상황에서 𝐵가 주어졌을 때, A의 조건부 확률은 아래 식과 같이 정리된다.

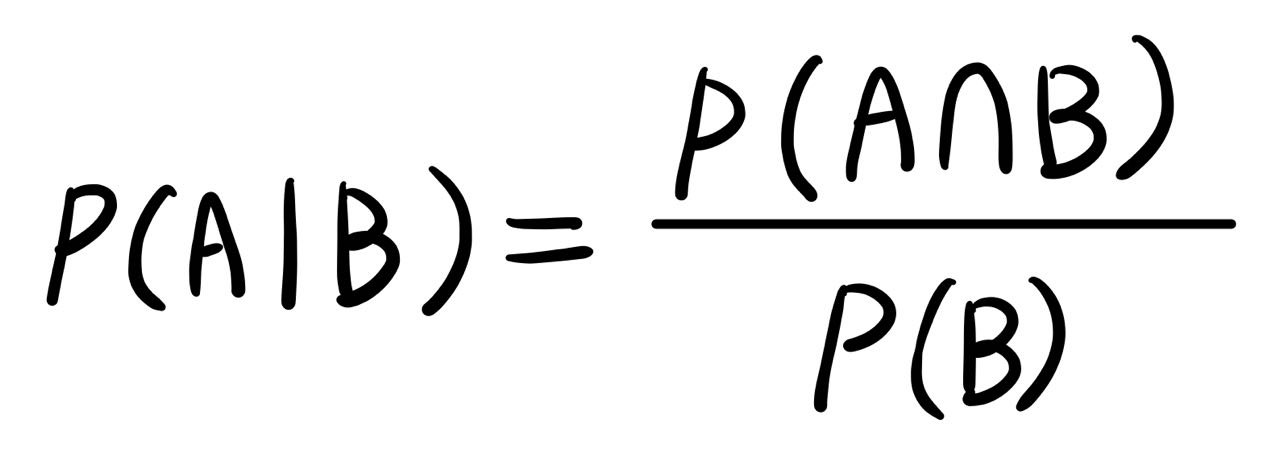
💡 조건부 확률은 𝐵라는 사건이 일어난 상황에서 사건 𝐴가 일어날 확률을 의미한다.

이 때 𝑃(𝐵) > 0 조건이 필요하다. 이 조건이 만족되지 않으면 정의에서 분모가 0이 되기 때문에 존재할 수 없어서 조건부 확률의 정의가 불가능하다.

 

3. 사건의 독립성

두 개의 사건 𝐴와 𝐵가 𝑃 𝐴 ∩ 𝐵 = 𝑃(𝐴)𝑃(𝐵)를 만족할 때 𝐴와 𝐵를 서로 독립이라고 한다.

 

확률분포

 

1. 확률변수

𝑥 ∶ 𝒳 → ℝ

확률변수는 표본공간에서 실수로 가는 함수로 표본공간의 원소를 실수로 대응시킨다.

💡 스크립트 𝓧는 복잡한 모양일 수 있기 때문에 실수인 ℝ로 단순화 시킨다 이때 쓰이는 것이 𝑥 확률변수다.

 

확률 변수 𝑥가 실수 상의 집합 𝐵에 포함될 확률로 실수 상에 정의된 확률 𝑃𝑥을 𝑃(𝑥 ∈ 𝐵) = 𝑃𝑥 (𝐵) 와 같이 정의할 수 있다. 이 때 𝑃𝑥를 확률 변수 𝑥의 분포(distribution)이라고 한다.

확률 𝑃는 표본 공간𝓧에 정의된 확률이고, 𝑥의 분포 𝑃𝑥 는 ℝ상에 정의된 확률이다.

 

2. 확률분포 표현의 세가지 방법

 

1) 확률

𝑥의확률분포𝑃는𝑥가포함된집합에대한확률을표시한다. 예를들면 𝐴 ⊂ 𝑅일때, 𝑥 ∈ 𝐴인확률을 𝑃(𝐴)혹은𝑃(𝑥 ∈ 𝐴)라표시한다

2) 누적분포함수

💡 실수에서 정의됐기 때문에 확률을 특징화 하는 것!

특징 짓는다는 것은 누적분포함수를 알면 확률을 결정할 수 있고 확률을 알면 누적분포함수를 결정할 수 있다는 뜻이다.

𝐹𝜃(𝑡) : = 𝑃𝜃 (−∞,𝑡) ,𝑡 ∈ ℝ

를 x의 누적분포함수(cumulative distribution function, cdf) 혹은 분포함수(distributionfunction)라 한다.

3) 확률밀도함수, 확률질량함수

💡 P(𝐴) 확률을 적분으로 표현하게 하는 𝑓(𝑥) 함수를 확률밀도함수라고 하고 합으로 표현할 수 있게 하면 확률질량함수라고 한다.

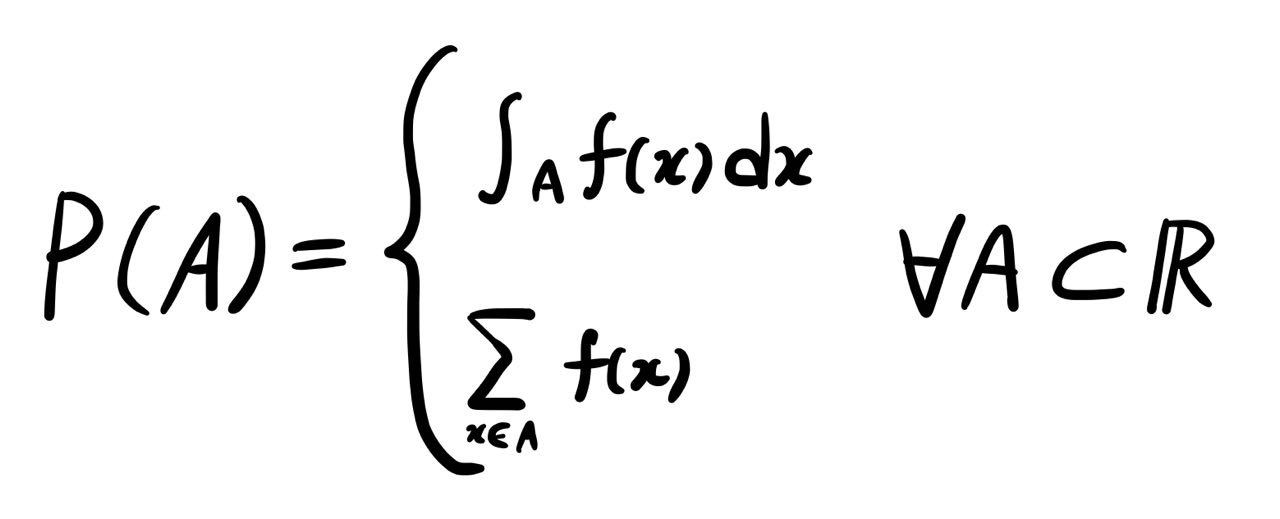
(확률밀도함수, 확률질량함수) 모든 𝐴 ⊂ ℝ에 대해서 확률을 0 보다 큰 값을 갖는 함수 𝑓 (𝑥)의 적분 혹은 합으로 위 식과 같이 표현할 수 있을 때 𝑓(𝑥)를 𝑥(혹은 𝑃)의 확률밀도함수(probability density function) 혹은 밀도함수(density function)라 한다. 확률을 확률 밀도 함수의 적분으로 표현할 수 있는 확률 변수를 연속형이라 하고, 합으로 표현할 수 있는 확률 변수를 이산형이라 한다. 이산형 확률 변수의 밀도 함수를 특별히 확률 질량 함수 (probability mass function)이라 하기도 한다.

 

3. 밀도함수의 변수 변환

확률 변수 𝑥의 확률 밀도 함수가 $𝑓_𝑥 (𝑥)$ 이고

로운 확률 변수가 𝑦 = 𝑢 𝑥 와 같이 정의되고

𝑢는 일대일 함수이고 연속적으로 미분 가능한 상태일 때

1) 𝑦의 확률 밀도 함수𝑓𝑦 (𝑦)를 다음과 같이 구할 수 있다.

2) ⅆ𝑥표현을 쓰면 𝑦에 대한 적분을 다음과 같이 쓸 수 있다.

 

+ 예제) 확률변수 𝑥의 밀도함수가 𝑓 (𝑥) = 2𝑥𝐼(0 < 𝑥 < 1) 일 때, 𝑦 = 𝑥 2의 밀도함수를 구하라.

 

4. 기댓값과 분산

기대값 확률 변수 𝑥의 확률 밀도 함수가 𝑓(𝑥) 일 때, 𝑢(𝑥) 의 기대값은 아래와 같이 정의된다.

기대값은 확률 측도 혹은 누적 분포 함수를 이용해서 아래와 같이 쓰기도 한다.

 

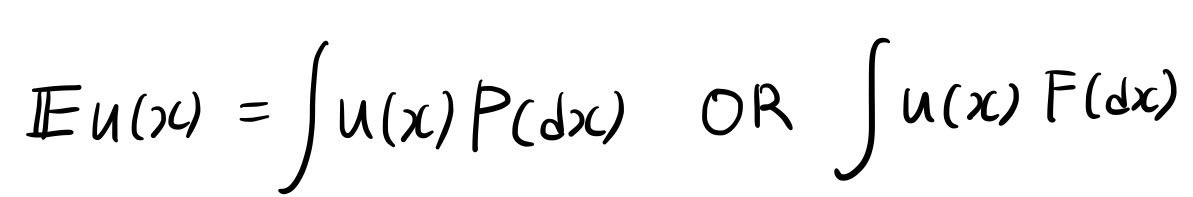
확률 변수 𝑥의 분산은 $𝕍𝑎𝑟(𝑥) = 𝔼 (𝑥 − 𝔼𝑥 )^2$ 로 정의되고

𝑥의 표준 편차는 𝑠ⅆ(𝑥) = $\sqrt{𝕍𝑎𝑟𝑥}$로 정의된다.

 

+ 예제) 확률변수 𝑢의 밀도함수가 𝑓 (𝑢) = 𝐼 (0 < 𝑢 < 1) 일 때, 𝑢의 평균을 구하라.