1. 일차연립방정식의 행렬 표현
- 행렬
: 행(row)와 열(column)로 구성되는 사각형 형태로 수를 배열한 것
- 행렬의 크기
: (행의 갯수)x(열의 갯수) = row by column
- m*n 행렬
행렬 A의 원소[성분]을 a[i, j]라고 한다.
- n원 일차연립방정식의 행렬
행렬방정식 AX = B
A : 계수행렬
X : 미지수행렬
B : 상수행렬
(A|B) : 확대행렬
2. 가우스 소거법
* 행렬에 관한 3가지 기본 연산
1) 두 행을 교환한다.
2) 한 행에 0이 아닌 상수를 곱한다.
3) 한 행에 임의의 상수를 곱하여 다른 행에 더한다.
- 기본행 연산(elementary row operation)
행렬 A에서 기본행연산을 통해 행렬 B를 얻을 수 있는 경우 A와 B는 행상등(row-equivalent)하다
일차연립방정식과 L1과 L2에 대해서 각각의 확대 행렬을 A와 B라 하였을 때, A와 B가 행상등 하면 L1과 L2는 상등하다.

행렬을 이용한 일차연립방정식의 해법
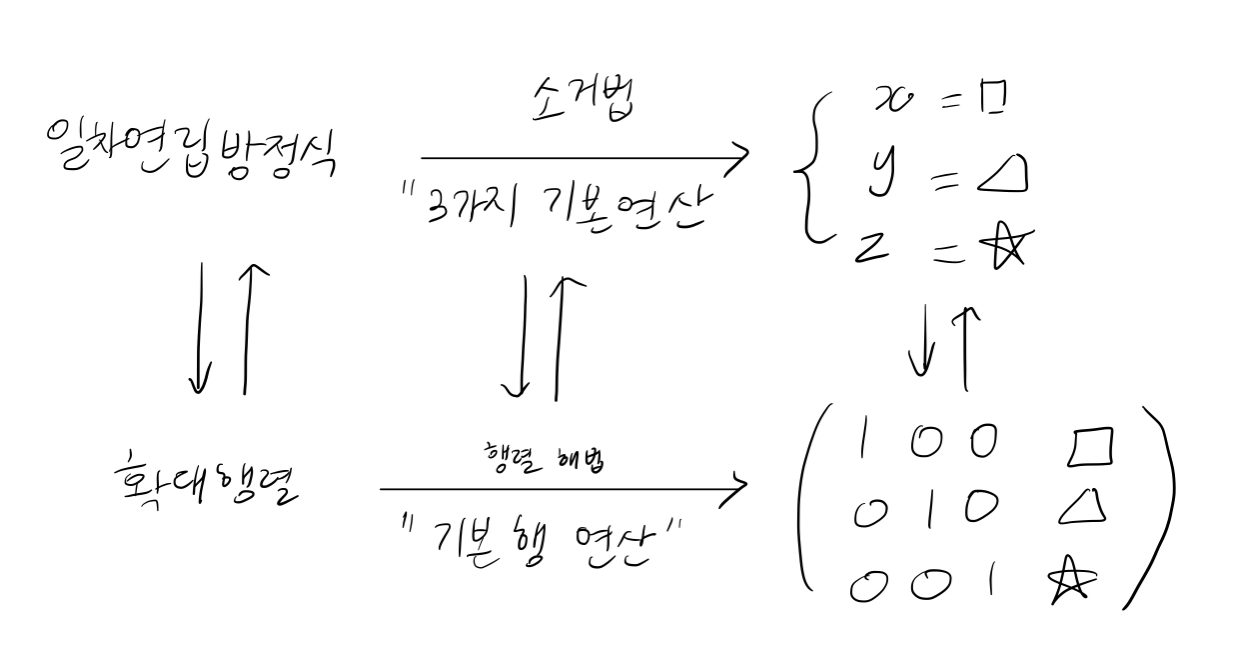
- 행제형 행렬(row echelon matrix)
1) 영행이 있다면 그것은 영행이 아닌 행의 아래에 있다.
2) 영행이 아닌 행의 첫 번째 0인 아닌 원소를 행의 선도원소라고 할 대 모든 선도원소는 1이다
* 선도원소 :
3) 영행이 아닌 연속된 두 행이 있어 각각 i번째 행과 i+1번째 행이라 할 때 i번째 행의 선도원소는 i+1번째 행의 선도원소보다 왼쪽에 있다(i>=1)
- 소거행제형 행렬(reduced row echelon matrix)
행제형 행렬이면서
4) i번째 행의 선도원소가 j번째 열에 있다면, j번째 열의 다른 모든 원소는 0이다
- 가우스 소거법
: 행제형 행렬을 구한 다음 후진대입법을 사용
- 가우스-조르단 소거법
: 소거행제형 행렬을 구하여 바로 해를 구함
3. 행렬 변환
- 행제형 행렬
- 소거행제형 행렬
'Computer Science > Math' 카테고리의 다른 글
| [선형대수학] 평면벡터와 공간벡터 (0) | 2021.11.21 |
|---|---|
| 크래머 공식 (0) | 2021.11.21 |
| [선형대수학]행렬식 (0) | 2021.11.21 |
| [선형대수학] 역행렬 (0) | 2021.11.21 |
| [선형대수학]행렬연산 (0) | 2021.11.20 |


댓글