1. 주성분분석이란?
서로 관련이 있는(즉, 상관계수가 0이 아닌) 변수들의 선형결합을 이용하여 새로운 변수를 만드는 과정이다.
즉, 원래 변수들이 가지고 있는 정보의 일정수준을 확보하도록 소수의 새로운 변수들을 만드는 방법으로 새로 만들어진 변수들이 서로 직교인 특성이 있다
분석 가장 강한 영향력을 가지고 있는 주된 변수의 갯수를 추려내는 것이다.
좀 전문적인 말로 쓴다면
서로 관련있는 변수들이 전체적으로 가지고 있는 정보들을 최대한 확보하는 적은 수의 새로운 주성분 변수를 생성하는 방법이다.
1) 주성분(principal component)이란?
다변량 자료가 가지고 있는 총변이의 주요부분을 함유하고 있는 성분을 의미한다.
2) 변이(variation)의 크기란?
- 정보의 크기를 나타내는 개념이다
- 일변량의 경우 분산으로 크기를 표현한다
다변량에서는 개별 변수들의 분산 외에 서로 다른 변수들 간의 공분산(혹은 상관계수) 이 추가된다.
어떤 현상을 연구할 때 관련된 변수가 있다.
관련된 변수가 두세개면 쉽게 산점도로 시각화 하고 현상에 대해 분석하고 예측하기 편하다.
만약 변수가 100개 이상으로 굉장히 많다면 모형화 하는 것도 어렵고 컴퓨터로 분석 돌리는 것도 굉장히 오래 걸리는 문제가 있다.
따라서 변수를 줄이는 방법을 고민해야한다.
분석 변수의 차원을 줄이는 Dimension reduction을 통해
서로 상관관계가 있는 변수들끼리 모아서 차원을 축소해 변수를 줄이는 분석 방법이다.
3) 주성분 분석의 목적
- 주성분분석은 다변량 변수들에 대한 단순화 하고, 서로 상관되어 있는 변수들 간의 내적 구조를 분석한다.
- 주성분분석은 원래변수들을 선형결합의 형식으로 변환시켜 주성분(principal component) 이라고 부르는 서로 상관되어 있지 않은(직교하는) 인공적 변수들을 유도한다.
- 각 주성분이 가지는 변이(정보)의 크기(주성분의 분산)를 기준으로 중요도를 고려해서 순서를 매긴다.
- 처음 몇 개의 주성분이 원래 자료가 가지고 있는 총변이(총정보)의 가능한 많은 부분을 보유하도록 함으로써 차원을 축약한다.
$$ PC = a_1 x_1 + a_{2} x_{2} +...+ a_{100} x_{100} $$

데이터가 분포해있는 곳에 주성분을 관통하는 가장 긴 선과 가장 짧은 선을 그리면 X1과 X2로 현상을 연구하는 것 보다
$PC_1$, $PC_2$로 대체해 설명할 수 있다.
$PC_1=a_1 X_1 + a_2 X_2$
$PC_2=b_1 X_1 + b_2 X_2$
이 경우 $PC_1$에 대한 분산이 $PC_2$보다 훨씬 크기 때문에 $PC_1$만 가지고도 대부분의 현상을 설명할 수 있다.
4) 주성분 구하는 방법
변수들의 분산 공분산행렬 S , 또는 상관계수행렬 R를 이용하여 구한다.
5) 먼저 분산 공분산행렬 S를 이용하여 주성분을 구해보자.
- 고유값 구하기
: 분산 공분산행렬 S는 5X5 대칭행렬이라고 가정했을 때 일반적으로 서로 다른 5개의 고유값, 고유벡터 쌍 5개가 존재한다.
아래 식에서 계수들을 주성분 계수라고 한다.
$ PC = a_1 x_1 $ + $a_2 x_2$ +...+ $a_100 x_100$
여기서 주성분이 갖는 모형의 분산은 a'Sa가 된다.

고유값은 ($S-\lambda )$의 행렬식(determination)을 만족하는 값이 되고
행렬식이 0이 되는 가장 큰 값을 $\lambda _1$ 이라고 한다.
여기서 $\lambda_1$ 에 대응되는 것을 $a_1$이라고 하고 $\lambda_2$ 에 대응되는 것을 $a_2$이라고 하면 직교하는 식을 구할 수 있다.
여기서 주성분이 갖는 모형의 분산은 a'Sa가 된다.
고유벡터는 각 고유값에 대응되는 값 A가 되고 이러한 주성분에 대해 고유값만 구하면 대부분을 설명할 수 있다.
* 고유값과 고유벡터란?
https://backenddeveloper.tistory.com/148
[Mulivariate Analysis] eigenvalue(고유값)과 eigenvector(고유벡터)
정방행렬 $A$에 대하여 $Ax = λx, Av=\lambda v$ (상수 λ) 가 성립하는 0이 아닌 벡터 x가 존재할 때 상수 λ 를 행렬 $A$의 고유값 (eigenvalue), x 를 이에 대응하는 고유벡터 (eigenvector) 라고 한다...
backenddeveloper.tistory.com
분산공산행렬에 고유값을 구하고 고유값에 대응되는 고유벡터로 구하게 되면
주성분의 계수가 된다.
람다가 분산이 되니까 전체 분산중에서 첫번째 주성분의 분산, 두번 째 주성분의 분산을 뽑은 후
첫번째 주성분이 갖는 분산이 설명하는 부분과 두번째 주성분의 분산이 설명하는 부분을 합쳤을 때 전체 분산의 합 대비 80% 이상이라면
두개의 주성분만 가지고 전체의 80%를 설명할 수 있다고 판단한다.
2. 주성분 분석 모형
주성분을 두개만 가지고 충분히 설명할 수 있다고 하면 주성분 이외의 부분에서 약간의 손실이 있다고 하더라도
큰 맥락의 흐름을 가지고 분석할 수 있다.
각 고유값에 대응하는 고유 벡터들을 직교화 했을 때 새로운 변수를 만들어낼 수 있기 때문에 고유값(eigenvalue)을 구해서 고유벡터(eigenvector)의 주성분 계수를 구할 수 있다

1) SVD(Singular Value Decomposition)
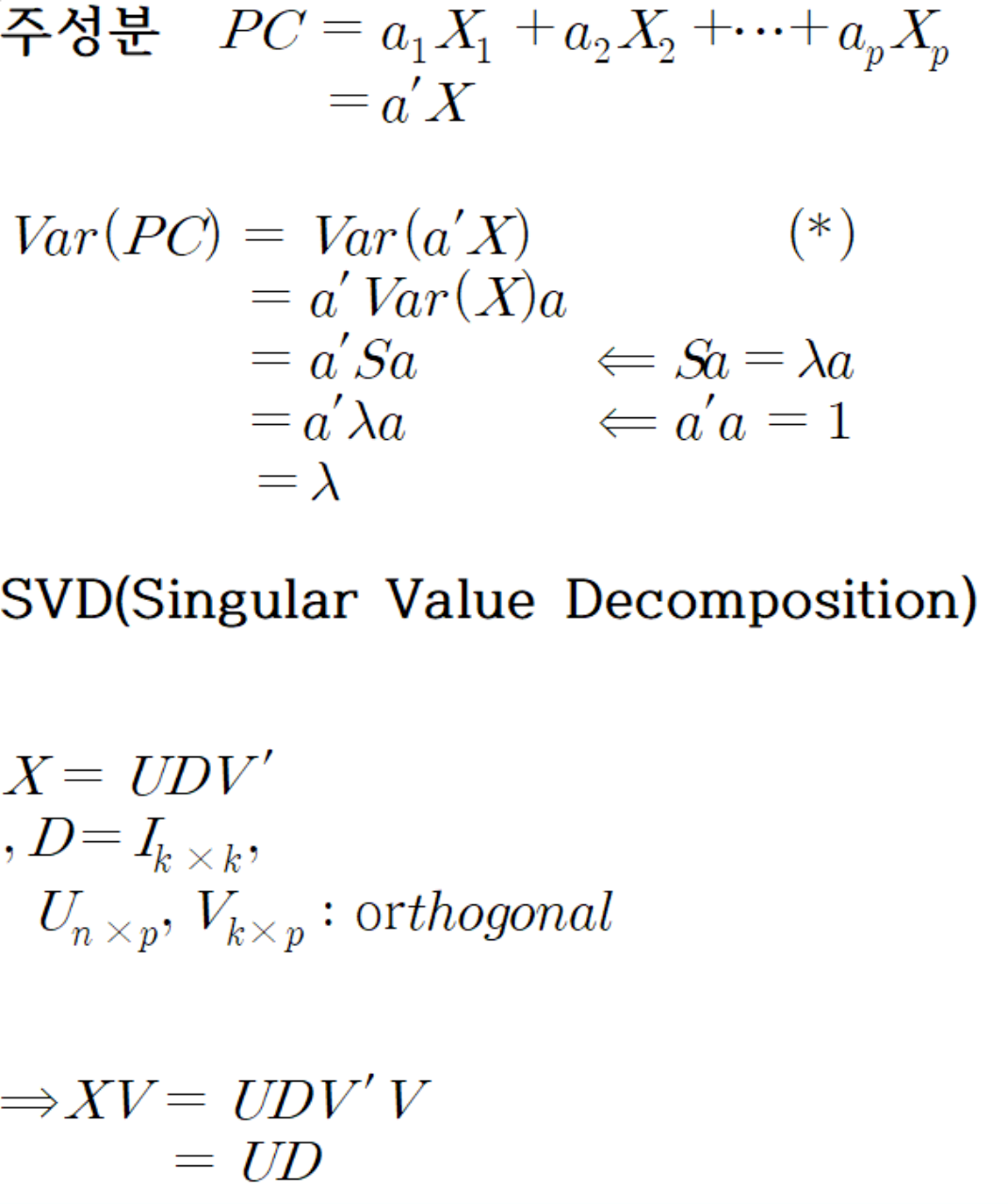

x 라고 하는 것을 분해할 때 udv’라고 하면
u’u=I가 단위행렬이 되고
v’v=I가 단위행렬이 될 때
D : diagoual matrix라고 한다.
x대신 시프트 시켜도 분산에는 변화가 없다.
x에서 xvar를 빼도 변함이 없어서
S=x’x라고 할 수 있고
x대신에 UDV’를 넣었을 때 S를 쉽게 구할 수 있다.
2) 주성분 적재 계수
주성분 적재 계수란 각 원래 변수와 차원 축약된 주성분변수와의 상관계수다.
- 주성분이 분산공분산행렬 S로부터 유도된 경우

- 주성분이 상관계수행렬 R로부터 유도된 경우

원래의 반응변수가 차원 축약된 주성분점수에 대한 영향 정도나 상관관계를 나타내는 통계량의 의미를 가진다.
3) 각 주성분들의 분산과 공분산
각 주성분을 정의하는데 이용된 고유 벡터들과 쌍을 이루는 고유값이 분산의 크기다.
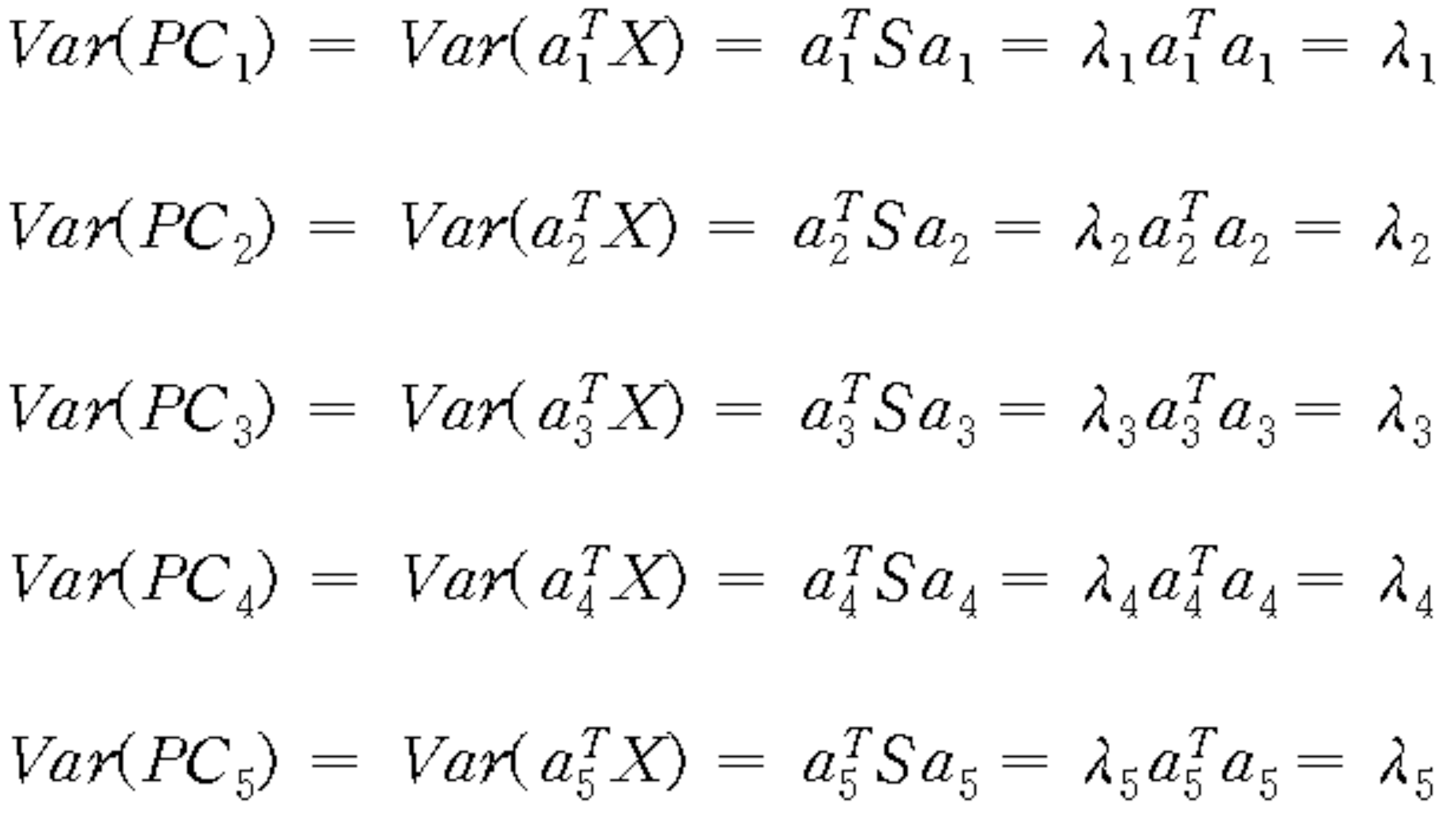
4) 두 주성분 사이의 공분산
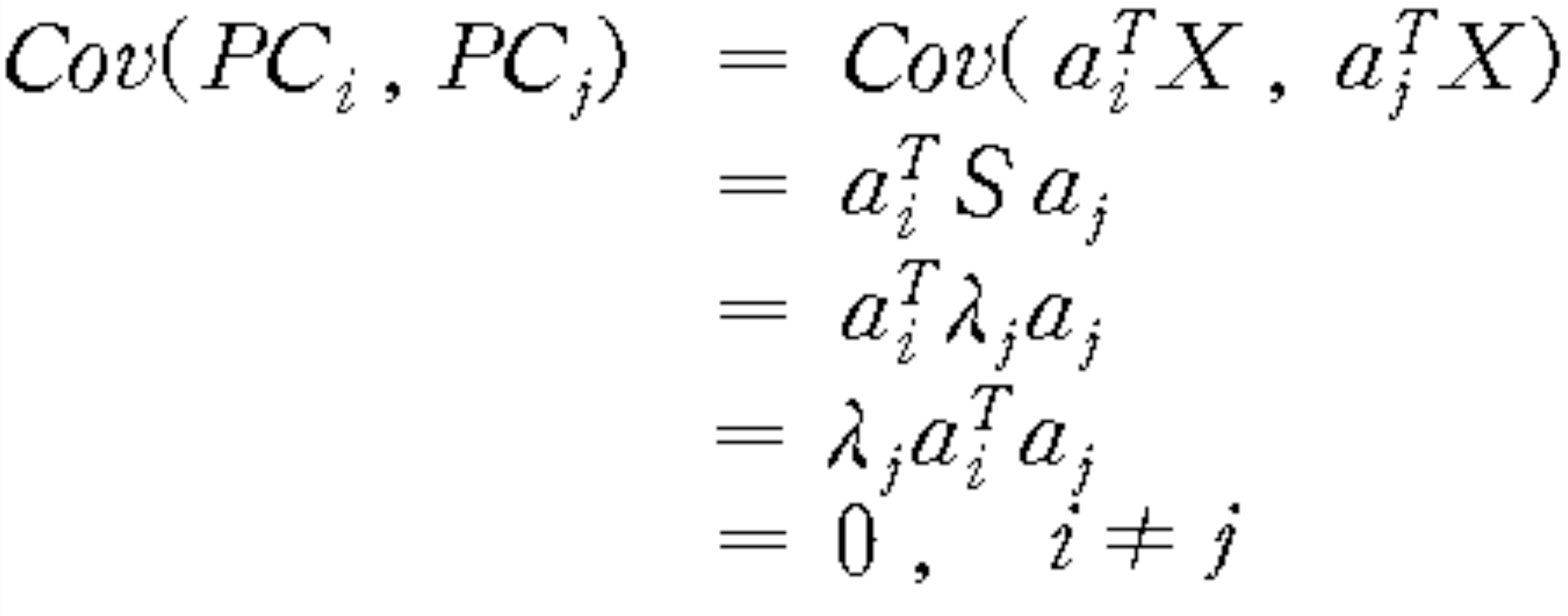
주성분 $PC_i$의 분산은 $\lambda_i$ i=1, 2, 3, 4, 5이며, 주성분은 서로 직교한다.
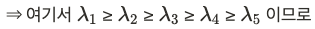
$PC_1$의 분산이 가장 크고 다음이 $PC_2$의 분산순서가 된다.
3. 표준화
각 계수의 단위가 다르다면 제대로 측정되지 않기 때문에 표준화를 한다.
보통 많이 쓰는 표준화는 Z스코어다.
공분산행렬을 바탕으로 고유값을 구하는데
공분산을 각각의 표준편차로 다시 나눠주면 상관계수가 된다
따라서 공분산 분산행렬이 상관계수 행렬이 된다.

위 식과 같이 표준화 하여 상관계수 행렬로 만든 것을 주성분 분석에 사용하게 된다.
주성분 수를 결정할 때 주성분의 분산의 크기를 확인하여
전체 고유값의 합 즉, 전체 분산의 합에 비해 원하는 크기 이상이 되면 해당 주성분들을 사용한다.
주성분으로 고려되기 위한 기준이 있는데 그의 분산인 고유값은 1보다 커야 한다는 kaiser’s 규칙이다.
이후 Jolliffe가 수많은 사례연구를 바탕으로 0.7 이상만 돼도 충분히 고려할만 하다는 의견을 냈고
주성분의 갯수와 상황에 따라 둘중 하나를 골라서 사용하면 된다.
'Data Science > Multivariate Analysis' 카테고리의 다른 글
| [Multivariate Analysis] Factor analysis(인자분석) (0) | 2022.03.21 |
|---|---|
| [Multivariate Analysis] 주성분분석 실행 with R, Python (0) | 2022.03.21 |
| [Mulivariate Analysis] eigenvalue(고유값)과 eigenvector(고유벡터) (0) | 2022.03.18 |
| [Multivariate Analysis] 다차원 통계그래프 (0) | 2022.03.13 |
| [Multivariate Analysis] 이변량 통계그래프 (0) | 2022.03.13 |




댓글