시계열의 요약
1. 시계열의 중심측도
- 표본평균

- 중앙값
크기순으로 나열할 때 중앙의 값이다.
특이값이 있을 경우 영향을 줄이기 위해 중앙값을 찾아서 평균을 계산하는데 도움을 준다.
- 최빈값
빈도가 가장 많은 값이다.
투표결과처럼 가장 많이 출현한 데이터를 측정한다.
2. 시계열의 산포
- 표본분산

- 표본 표준편차

- 사분위편차
특이값의 영향을 줄이기 위해 중심값을 확인하여 보정하는 것이다.

3. 시계열의 사례
- 경제성장률 추이
GDP는 계절조정계열과 원계열 두가지 형태로 발표된다.
경제성장률은 계정조정계열의 전기대비 증감률로 확인한다.
시계열의 분포
1. 시계열분포란?
시계열 값들이 얼마나 퍼져있고 공통점을 가지고 있는지 개형을 파악하는 것이다.
- 히스토그램(histogram)
- 확률밀도함수 : 히스토그램을 평활화해서 확률밀도함수를 추정할 수 있다.
2. 경제성장률의 확률분포

3. 종합주가지수 로그차분의 확률분포
금액에 가중평균방식으로 지수를 만들어서 분포를 시켰다.
로그차분은 로그수익률이라고 해석할 수 있다.
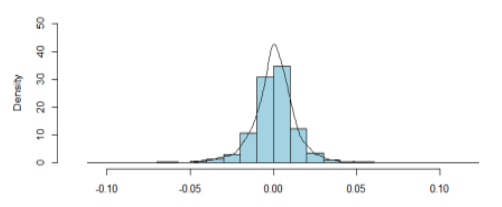
4. 정규분포
시계열 분포가 정규분포와 같은건지 알아보자
뮤를 중심으로 좌우대칭이다.
좌우대칭과 종모양으로 분포하는 정규분포와 공통적인 특성을 가진다.
5. 정규성 검정
1) Jarque-Bera(자크-베라) 검정
- 첨도 : 얼마나 뾰족하고 선명하게 나오는지의 정도를 말한다.
- 왜도 : 비대칭성을 말한다.
2) 샤피로-윌크스 검정
3) KS검정
4) qqplot
...
자기상관
1. 표본상관계수
시계열은 시간영역과 주파수 영역의 정보로 나눠진다.
시간영역은 시계열의 과거->현재->미래의 연결구조를 이해하는 것이다.
주파수정보는 순환하는 사이클을 말한다.
표본상관계수란?
두 변수의 움직임을 통해서 변수의 관계를 파악하는 것이다.

- r > 0 : 두 변수가 같은 방향으로 움직임
- r < 0 : 두 변수가 반대반향으로 움직임
- r = +-1 : 완전 선형관계
- r = 0 : 선형관계가 없음
2. 표본 자기상관계수
1) 표본자기상관계수란?
시차변수 간 표본 상관계수를 말한다.

- 이론적 자기상관계수
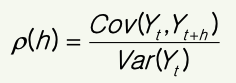
2) 표본자기상관계수의 분포
시계열이 서로 독립적이고 동일한 분포를 나타낸다.
백색잡음계열이라고도 한다.
3) 표본자기상관계수의 검정
- $H_0$ 귀무가설과 $H_1$ 대립가설을 세운다.
ex) 자기상관계수가 실제로 0.1이 나왔는데 이것을 0과 같다고 볼 수 있을지 검정하는 것
$H_0$ 귀무가설은 0이 유의하다!
$H_1$ 대립가설은 0이 유의하지 않다!

-기각역을 통해 귀무가설을 기각한다.

3. 상관도표
1) 상관도표란?
시차별 표본 자기상관계수의 그래프다.
아래 그래프에서 5% 유의수준의 기각역으로 0이 유의하지 않다는 것을 확인하였다.
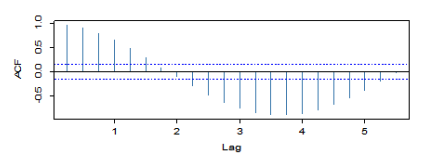
- x축 : 시차(h)
- y축 : 표본 자기상관계수
2) 백색잡음계열의 상관도표
정규분포로부터 나온 백색잡음계열 도표다.
95%의 기각역인 아주 작은 값이 된다.

3) Sin 커브의 상관도표

4) GDP 원계열의 상관도표

5) GDP(원계열) 로그차분계열의 상관도표
데이터를 로그차분 했을 때 추세는 사라지고 계절성만 남는다.
도표를 보면 서서히 없어지는 추세는 사라지고 값들이 지그재그로 보인다
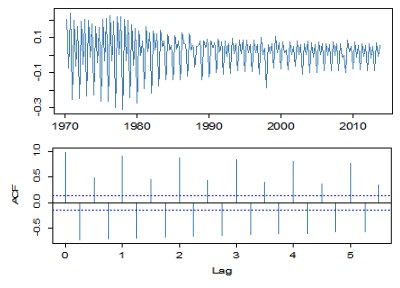
4. 륭-박스 검정
1) 륭-박스의 검정이란?
시계열에 자기상관 관계가 존재하지 않으면 랜덤한것과 대응된다.
자유도가 0인 카이제곱 분포를 따라 계산한다.
- m개의 자기상관이 모두 0이라는 귀무가설을 검정한다.
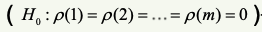
- 만약 $Q_m > X^2_{m,a}$이면 유의수준 $\alpha$에서 귀무가설을 기각한다.
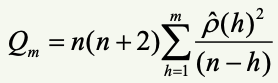
2) 륭-박스 검정 결과
유의확률은 귀무가설을 참으로 두고 검정통계량에 대한 유의확률의 값을 구해 판단한다.
일반적으로 5%를 사용하기 때문에 유의확률이 0.05보다 작으면 귀무가설을 기각하고 0.05보다 크면 귀무가설이 유의하다고 판단한다.
| 계열명 | 검정통계량값 | 유의확률(p-value) |
| 백색잡음계열 | 3.16 | 0.92 |
| Sin계열 | 497.65 | < 2.2e-16 |
| GDP원계열 | 1249.76 | < 2.2e-16 |
| GDP 로그차분계열 | 756.05 | < 2.2e-16 |
| GDP로그 4차 차분계열 | 205.63 | < 2.2e-16 |
'Data Science > Forecasting' 카테고리의 다른 글
| [Forecasting] 부분자기상관과 시계열의 주파수 분석 (0) | 2022.04.20 |
|---|---|
| [Forecasting] 예측 데이터 (3) | 2022.04.06 |
| [Forecasting] 예측이란? (4) | 2022.04.05 |



댓글