회귀선의 추정
1) 회귀선
회귀선은 표본자료(Sample data)로부터 모형식을 추정하여 얻은 직선으로 아래와 같은 공식을 가진다.
$\hat{Y} = b_0 + b_1X$
$b_0$, $b_1$은 각각 $\beta_0, \beta_1$ 의 추정값
$\hat{Y}$ 은 주어진 X에서의 기댓값 $E(Y)$ 의 추정값
$b_0$ 는 $X = $ 일 때, $\hat{Y}$ 의 값으로 추정된 회귀절편(intercept)
$b_1$ 는 X가 한 단위가 증가할 때에 $\hat{Y}$ 의 증가량 => 기울기(slope)
$\hat{Y_1} = b_0 + b_1(X+1)$ 이면 $b_0 + b_1X + b_1$으로 $b_1$이 증가한다.
2) 최소제곱법(Method of Least Squares)
회귀계수 $b_0$와
최소제곱법을 이용하여 모수를 추정하는 방법
최소제곱법
$Y_i - \beta_0 - \beta_1X_i = \epsilon_i$
에서 오차제곱들의 합을 구하면
$S = \sum_{i=1}^{n} (Y_i - \beta_0 - \beta_1X_i)^2$
최소로 하는 $\beta_0$와 $\beta_1$의 값들을 이들의 추정값 $b_0$ 와 $b_1$ 으로 하는 방법
오차제곱합 $S$를 최소화시키는 $\beta_0$와 $\beta_1$의 값을 구하기 위하여 S를 $\beta_0$와 $\beta_1$ 두 모수로 각각 편미분 한다.
$\frac{\partial S}{\partial B_0} = -2\sum(Y_i - B_0 - B_1X_i)$
$\frac{\partial S}{\partial B_1} = -2\sum X_i(Y_i - B_0 - B_1X_i)$
편미분값을 0으로 만드는 $\beta_0$ 와 $\beta_1$ 을 각각 $b_0$ 와 $b_1$ 으로 대체하여 정리하면,
[$b_0$]
$ {-2}\sum(Y_i - b_0 - b_1X_i) = 0 $
-> $b_0n + b_1\sum X_i = \sum Y_i$
[$b_1$]
$ {-2}\sum X_i(Y_i - \beta_0 - \beta_1X_i) = 0$
-> $b_0\sum X_i + b_1\sum X_i^2 = \sum X_iY_i$
이런 정규방적식을 얻게 되는데 이차방정식으로 놓고 풀면 된다.
$\large{b_1 = \frac{\sum(X_i - \overline{X})(Y_i - \overline{Y})}{\sum(X_i - \overline{X})^2}}$
$b_0 = \overline{Y} - b_1\overline{X}$
최소제곱법추정된 $\hat Y$에대한 회귀식은 반드시 두 평균을 지나면서 기울기가 $b_1$인 직선방정식을 얻을 수 있다.
- 기울기 : $b_1={S_{xy} \over S_{xx}}$
- 절편 : $b_0=\bar Y-b_1\cdot\bar X$
(예) 표본상점의 광고료와 총판매액 자료에 대하여 회귀직선을 구하고, 산점도 위에 회귀직선 그려보기.
> market.lm = lm(Y~X, data=market)
> summary(market)
NUMBER X Y
Min. : 1.00 Min. : 4.0 Min. : 9.0
1st Qu.: 3.25 1st Qu.: 6.5 1st Qu.:15.5
Median : 5.50 Median : 8.0 Median :19.0
Mean : 5.50 Mean : 8.0 Mean :18.6
3rd Qu.: 7.75 3rd Qu.: 9.0 3rd Qu.:21.5
Max. :10.00 Max. :12.0 Max. :30.0
> summary(market.lm)
Call:
lm(formula = Y ~ X, data = market) #회귀모형식
Residuals:
Min 1Q Median 3Q Max
-3.600 -1.502 0.813 1.128 4.617 #잔차
Coefficients: #계수 이 계수가 우리가 구하고자 하는 회귀식을 보여줌
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.2696(절편) 3.2123 -0.707 0.499926
X 2.6087(기울기) 0.3878 6.726 0.000149 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.631 on 8 degrees of freedom
Multiple R-squared: 0.8497, Adjusted R-squared: 0.831
F-statistic: 45.24 on 1 and 8 DF, p-value: 0.0001487- Estimate을 보면 추정된 회귀식을 구할 수 있다.
- (Intercept)은 절편에 대한 값이다.
추정된 회귀식
$$ \hat Y=2.2696+2.6087X $$
3) 산점도 그리고 위에 기울기가 $b_1$인 직선 추가
# 산점도 그리기
plot(market$X, market$Y, xlab="advertisement fee", ylab="total sales", pch=19)
title("Scatterplot of Advertising Fees and Sales")
# 직선 그리기
abline(market.lm)
# row name 확인용 (마우스 우클릭으로 선택 가능)
identify(market$X, market$Y)
4) 잔차(residual)
잔차는 $X_i$에서 측정된 값 $Y_i$와 추정된 $\hat Y_i$ 과의 차이다,
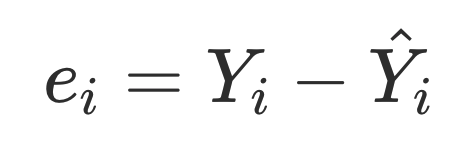
- 잔차들의 합은 0이 된다.
즉, $\sum e_i = 0$ - 잔차제곱의 합, $\sum e_i^2$ 은 최소가 된다.
제곱을 해주는 이유는 마이너스를 없애주기 위해서다. - 잔차가 0이 되니까 관찰값 $Y_i$ 의 합과 추정값 $\hat{Y_i}$ 의 합은 같다.
즉, $\sum Y_i = \sum\hat{Y_i}$
> names(market.lm)
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign" "qr"
[8] "df.residual" "xlevels" "call" "terms" "model"
> resid = market.lm$residuals
> fitted = market.lm$fitted
> sum(resid) # 잔차들의 합이 0인지 확인
[1] 0
> sum(fitted) # 추정값의 합이 0인지 확인
[1] 186
> sum(market$Y)
[1] 186names를 하게 되면 "residuals"와 추정값인 "fitted.values" 등의 변수를 확인할 수 있다.
- 잔차들의 $X_i$ 에 의한 가중합은 0.
즉, 잔차를 독립변수로 곱한 것의 가중합은 $\sum X_ie_i = 0 $
이것은 $X\bot e$ $X$와 $e$는 수직이라는 뜻이다. - 잔차들의 $\hat{Y_i}$ 에 의한 가중합도 0.
즉, $\sum \hat{Y_i}e_i = 0$
> names(market.lm)
[1] "coefficients" "residuals" "effects" "rank" "fitted.values" "assign" "qr"
[8] "df.residual" "xlevels" "call" "terms" "model"
> sum(market$X*resid)
[1] 2.220446e-15 #2.220x10^-15 이므로 0이 되는 것을 확인할 수 있다.
> sum(fitted*resid)
[1] -1.24345e-14
- 점 ($\overline{X}$, $\overline{Y}$) 는 적합된 회귀선상에 존재함.
즉, $\hat{Y_i} = \overline{Y} + b_1(X_i - \overline{X})$</li>
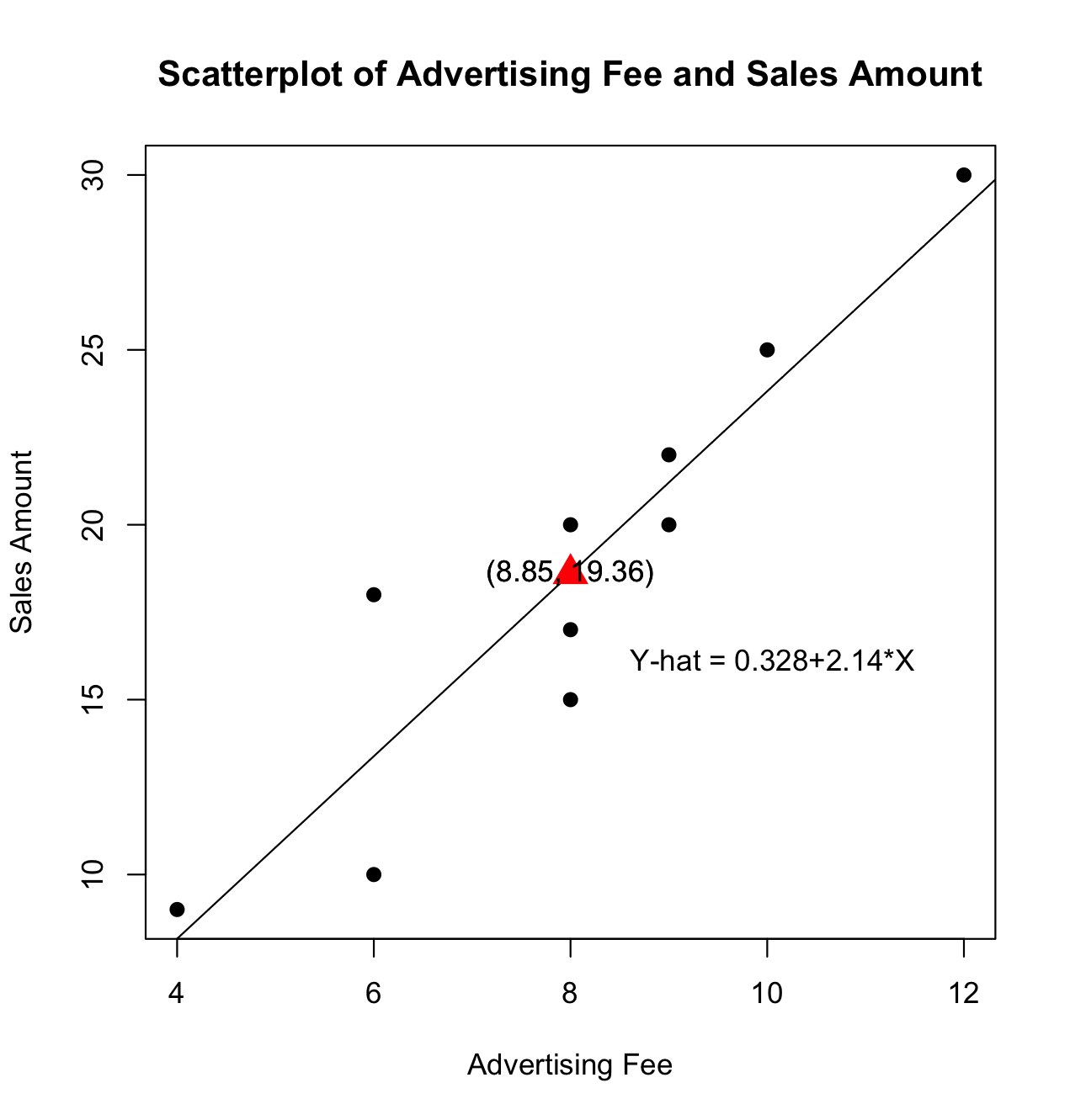
> plot(market$X, market$Y, xlab="Advertising Fee", ylab="Sales Amount", pch=19) # 산점도 그리기
> title("Scatterplot of Advertising Fee and Sales Amount")
> abline(market.lm) # 회귀선 구하기
> xbar = mean(market$X) #x평균값
> ybar = mean(market$Y) #y평균값
> xbar
[1] 8
> ybar
[1] 18.6
> points(xbar, ybar, pch=17, cex=2.0, col='RED') #해당 부분에 점 찍기
Error: unexpected input in "points(xbar, ybar, pch=17, cex=2.0, col='RED' #""로 감싸서 RED가 깨졌었는데 ''로 감싸니까 잘 나옴
> text(xbar, ybar, "(8.85, 19.36)")
> fx <- "Y-hat = 0.328+2.14*X"
> text(locator(1), fx) #내가 마우스 클릭으로 지정한 위치에 찍어주는 기능xbar, ybar는 회귀선상 위에 반드시 있는 것을 확인할 수 있다.
'Data Science > Regression Analysis' 카테고리의 다른 글
| [Regression] 가중회귀 (0) | 2022.03.31 |
|---|---|
| [Regression] 회귀계수의 신뢰구간 및 검정 방법 (0) | 2022.03.30 |
| [Regression] 회귀모형의 평가 분산분석(ANOVA) (0) | 2022.03.11 |
| [Regression] 단순회귀모형 (0) | 2022.03.09 |
| [Regression] 회귀분석이란? (0) | 2022.03.04 |




댓글