기본적인 오차제곱의 이해

분산분석표에 의한 F-검정
분산분석표는 변동을 분해한 표다.
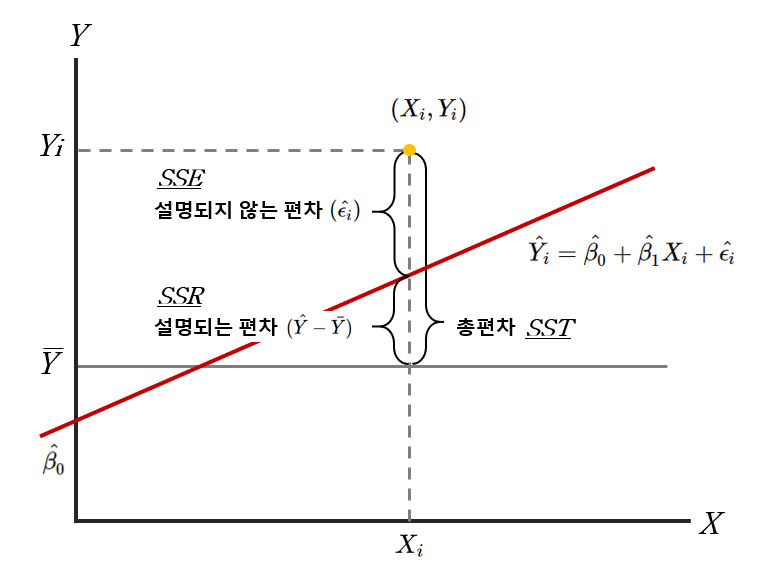
결정계수 $R^2$는 총제곱합 중에서 회귀 제곱합이 차지하는 비중에 대한 설명이다.
| 종속변수 관련 값 | |||
| $\hat{Y}$ | 예측된 종속변수의 값 | ||
| $\bar{Y}$ | 예측된 종속변수들의 평균값 | ||
| $Y_i$ | 실제 관측치 | ||
| 적합도 검정($R^2$을 계산)을 위한 값 | |||
| 총편차 | $Y_i-\bar{Y}$ | 총제곱합(SST) | $\sum{(Y_i-\bar{Y})^2}$ |
| 설명되는 편차 | $\hat{Y}-\bar{Y}$ | 회귀 제곱합(SSR) | $\sum{(\hat{Y}-\bar{Y})^2}$ |
| 설명되지 않는 편차 | $Y_i-\hat{Y}$ | 오차 제곱합(SSE) | $\sum{(Y_i-\hat{Y})^2}$ |
| 설명력을 나타내는 결정계수 : $R^2$ 계산 | |||
| $SST = SSE + SSR \rightarrow \frac{SSR}{SST}=1-\frac{SSE}{SST}$ | |||
$\sum(Y_i - \overline{Y})^2 = \sum(\hat{Y_i} - \overline{Y})^2 + \sum(Y_i - \hat{Y_i})^2$
$SST = SSR + SSE$
총제곱합 = 회귀제곱합 + 잔차제곱합
total sum of squares = residual sum of squares + explained sum of squares
자유도 $(n-1) = (n-2) + 1
변동의 분해는 분산의 총제곱합을 회귀, 잔차의 제곱합으로 분해하고 이러한 제곱합은 항상 자유도를 갖게 된다.
총제곱합의 자유도는 총 데이터수에서 평균에 대한 1을 뺀 것이다.
잔차제곱합의 자유도는 n-2
회귀제곱합의 자유도는 독립변수 1이다.
이런 변동에 대한 분해를 정리한 것을 분산분석표라고 한다.
<단순회귀의 분산분석표>
이 회귀모형이 유의한지 설명력이 얼마나 되는지를 알 수 있다.
| 요인 |
자유도 (Degree of Freedom) |
제곱합 (SS, Sum of Square) |
제곱평균 (MS, Mean of Square) |
$F_0$-통계량 (F-Value) |
P-값 (P-Value) |
| 회귀 (Regression) | 1 | 회귀제곱합 (SSR) |
회귀제곱평균 (MSR) MSR = SSR / k |
F비 MSR / MSE |
F-통계량의 유의확률 (F분포표) |
| 잔차 (Error) | n - 2 | 잔차제곱합 (SSE) |
잔차제곱평균 (MSE) MSE = SSE / (n - 2) |
||
| 총 (Total) | n - 1 | 총제곱합 (SST) SSR + SSE |
총제곱평균 (MST) MST = SST / (n - 1) |
제곱합을 자유도로 나눠준 것을 평균제곱이라 한다.
- 가설검정
$H_0 : \beta _1 = 0$
$H_1 : \beta _1 != 0$
- 검정통계량
$F_0 = \frac{MSR}{MSE}$
검정통계량 $F_0$은 회귀의 평균제곱을 잔차의 평균제곱으로 나눈 것이다.
- 검정방법
$F_0 > F(1, n -2; \alpha)$ 이면 귀무가설을 기각하고 추정한 회귀직선이 유의하다고 할 수 있다.
위의 분산분석표에 의한 검정통계량을 가설검정에 기각역으로 사용할 수 있다.
p값을 제공해주는데 유의확률 p값이 작을수록 가설을 기각할 수 있다.
- R에서는 검정통계량 $F_0$에 대한 유의확률 p-값이 제공된다.
"p-값 < 유의확률 $\alpha$"면 귀무가설을 기각한다.
> market.lm = lm(Y ~ X, data=market)
> anova(market.lm)
Analysis of Variance Table
Response: Y
Df Sum Sq Mean Sq F value Pr(>F)
X 1 313.043 313.04 45.24 0.0001487 ***
Residuals 8 55.357 6.92
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1분산분석 결과를 해석하면 $p-값=1.487*10^{-9}$ 로 매우 작은 값이므로 $H_0 : \beta _1 = 0$을 기각
Df : 자유도
Sum Sq : 제곱합
Mean Sq : 평균제곱
Pr : 유의확률
결정계수
추정된 회귀선이 얼마나 설명력이 있는지 알기 위해 수치로 나타내서 얼만큼 있는지 상대적으로 비교해볼수 있다.
결정계수(coefficient of determination)는 총변동중에서 추정된 회귀선이 설명할 수 있는 비율을 나타내는 것이며, 회귀선의 기여율이라고 부르기도 한다
$R^2 = \frac{SSR}{SST} = 1 - \frac{SSE}{SST}$
$R^2$의 범위는 $0 \leqq R^2 \leqq 1$ 이다.
결정계수 값은 0에서 1사이에 있으며 X와 Y 사이에 높은 상관관계가 있을수록 $ 값은 1에 가까워진다.
$ 값이 1에 가까워질수록 설명력이 높은 회귀선이다.
> market.lm = lm(Y ~ X, data=market)
> anova(market.lm)
Analysis of Variance Table
Response: Y
Df Sum Sq Mean Sq F value Pr(>F)
X 1 313.043 313.04 45.24 0.0001487 ***
Residuals 8 55.357 6.92
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1$=> R^2=313.043/(313.043+55.357)=0.8497$
이는 총변동 중에서 회귀직선에 의해 설명되는 부분이 84%라는 의미다.
추정된 회귀선의 정도가 높지 않다는 것을 알 수 있다.
결정계수는 값이 클수록 유리하다
추정값의 표준오차
$σ^2$ : 오차분산
$
위의 분산분석표에서 잔차평균제곱 MSE는 오차분산 $\sigma^2$ 의 불편추정량이 된다.
따라서 MSE의 제곱근을 추정값의 표준오차(Standard Error of Estimate)이라고 부른다.
$S_{Y*X} = \sqrt{MSE}$
추정값의 표준오차는 주로 두 모형의 비교에서 더 작은 값을 가진 모형이 주어진 자료에 더 적합하다는 의미로 이용된다.
> market.lm = lm(Y ~ X, data=market)
> summary(market.lm)
Call:
lm(formula = Y ~ X, data = market)
Residuals:
Min 1Q Median 3Q Max
-3.600 -1.502 0.813 1.128 4.617
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.2696 3.2123 -0.707 0.499926
X 2.6087 0.3878 6.726 0.000149 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.631 on 8 degrees of freedom
Multiple R-squared: 0.8497, Adjusted R-squared: 0.831
F-statistic: 45.24 on 1 and 8 DF, p-value: 0.0001487> anova(market.lm)
Analysis of Variance Table
Response: Y
Df Sum Sq Mean Sq F value Pr(>F)
X 1 313.043 313.04 45.24 0.0001487 ***
Residuals 8 55.357 6.92
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1=> $S_{Y*X} = \sqrt{MSE} = \sqrt{6.92} = 2.63$
단순회귀모형에서 상관계수와 결정계수의 관계
- 상관계수
두 연속인 변수 간의 선형관계(linear relationship)가 어느 정도인가를 재는 측도다.
$\begin{align} r &= \frac{\sum(X_i - \overline{X})(Y_i - \overline{Y})}{\sqrt{\sum(X_i - \overline{X})^2\sum(Y_i - \overline{Y})^2}} &= \frac{S_{XY}}{\sqrt{S_{XX}S_{YY}}} \end{align}$
단순회귀모형에서 상관계수 r과 결정계수의 관계는 아래와 같다.
$r = \pm \sqrt{R^2}$
만약 추정된 회귀선의 기울기 $b_1$이 양이면 $r = \sqrt{R^2}$ 이므로 양의 상관계수를 갖고
만약 추정된 회귀선의 기울기 $b_1$이 음이면 $r = - \sqrt{R^2}$이므로 음의 상관계수를 갖는다.
'Data Science > Regression Analysis' 카테고리의 다른 글
| [Regression] 가중회귀 (0) | 2022.03.31 |
|---|---|
| [Regression] 회귀계수의 신뢰구간 및 검정 방법 (0) | 2022.03.30 |
| [Regression] 회귀선의 추정 (0) | 2022.03.09 |
| [Regression] 단순회귀모형 (0) | 2022.03.09 |
| [Regression] 회귀분석이란? (0) | 2022.03.04 |




댓글