1. 단순회귀의 추정과 검정
기울기에 대한 추정값 $b_1$과 절편에 대한 추정값 $b_0$을 이용해 구간추정과 가설검정을 한다.

정규분포를 따른다고 가정할 수 있다.
따라서 관측되는 값들이 전부 회귀선과 가까이 있다면 분산의 추정값은 작아진다.
2. $\beta_1$의 신뢰구간
- 회귀계수 기울기 $\beta_1$의 추정량

- 기댓값, 분산

- $\sigma^2$의 추정값은 MSE에 의하여 구해짐

- $b_1$의 분산에 대한 추정값

- $\beta_1$의 신뢰계수 100(1-$\alpha$)% 신뢰구간

- 절편 $\beta_0$의 추정량
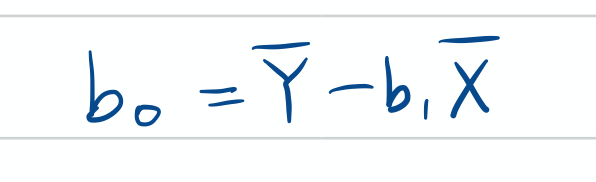
- 기댓값 및 분산

- $\beta_0$의 100(1-$\alpha$)%의 신뢰구간

3. R 결과에서 $\beta_1$과 $\beta_0$ 신뢰구간 구하기
> market.lm = lm(Y ~ X, data=market)
> summary(market.lm)
Call:
lm(formula = Y ~ X, data = market)
Residuals:
Min 1Q Median 3Q Max
-3.600 -1.502 0.813 1.128 4.617
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.2696 3.2123 -0.707 0.499926
X 2.6087 0.3878 6.726 0.000149 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.631 on 8 degrees of freedom
Multiple R-squared: 0.8497, Adjusted R-squared: 0.831
F-statistic: 45.24 on 1 and 8 DF, p-value: 0.0001487$\beta_1$의 95% 신뢰구간
> q.val=qt(0.975,13)
> 2.6087-q.val*0.3878
[1] 1.770909
> 2.6087+q.val*0.3878
[1] 3.446491$\beta_0$의 95% 신뢰구간
> q.val=qt(0.975,13)
> -2.2696-q.val*3.2123
[1] -9.209352
> -2.2696+q.val*3.2123
[1] 4.670152
4. 추정값의 신뢰구간
어떤 주어진 값 X에서 Y의 기대값을

라고 하면, 이는 다음과 같이 추정된다.
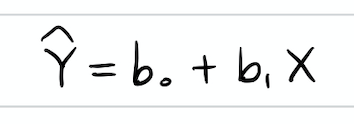
1) 추정량$\hat Y$의 기댓값 및 분산

이렇게 유도한 식으로 신뢰구간을 구할 수 있다.

=> $\hat Y$의 분산은 X의 함수로서 $X=\bar X$일 경우에 최소가 되며,
$X=\bar X$를 대칭으로 X의 값이 $\bar X$에서 멀어질수록 분산이 커진다.
또한 표본의 크기 n이 커져도 Var($\hat Y$)이 작아지는 것을 알 수 있다.
2) 예측값의 신뢰구간
주어진 X의 값에서 새로운 예측값 $Y_{new}$의 신뢰구간
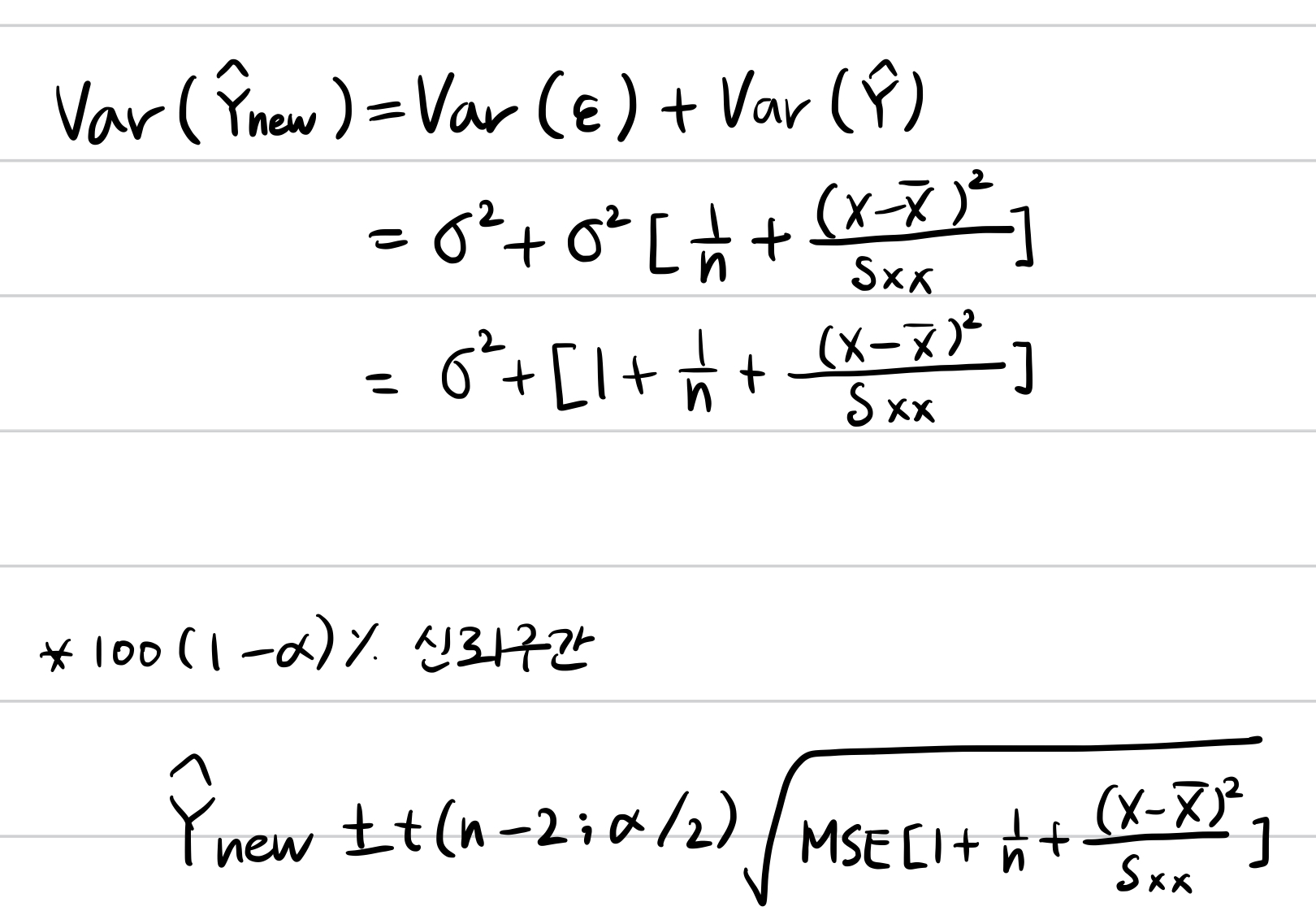
추정값에 대한 분산을 더해주게 되면 1만큼 커진다.
새로운 예측값 y의 신뢰구간은 오차항의 분산을 더해서 추정한다.
- 모집단 회귀모형의 오차항은 평균이 0이고 분산이 σ2인 정규분포를 따른다고 가정했을 때 회귀계수 α, β와 그 외 모수에 대해 추론할 수 있다.
3) 신뢰대 그리기
X의 주어진 값에서 신뢰대 그리기
> pred.frame = data.frame(X=seq(3.5, 14.5, 0.2))
> # 기댓값 신뢰구간
> pc = predict(market.lm, int="c", newdata=pred.frame)
> # 예측값 신뢰구간
> pp = predict(market.lm, int="p", newdata=pred.frame)
> head(pc, 3)
fit lwr upr
1 6.860870 2.402421 11.31932
2 7.382609 3.084944 11.68027
3 7.904348 3.765982 12.04271
> head(pp, 3)
fit lwr upr
1 6.860870 -0.66731914 14.38906
2 7.382609 -0.05148732 14.81670
3 7.904348 0.56119219 15.24750위에서 구한 pp, pc로 x변수와 y변수의 산점도를 그린다.
범위를 충분히 잡아주기 위해서 range 사용한다.
> pred.X = pred.frame$X
> pred.X
[1] 3.5 3.7 3.9 4.1 4.3 4.5 4.7 4.9 5.1 5.3 5.5 5.7 5.9 6.1 6.3 6.5 6.7 6.9 7.1
[20] 7.3 7.5 7.7 7.9 8.1 8.3 8.5 8.7 8.9 9.1 9.3 9.5 9.7 9.9 10.1 10.3 10.5 10.7 10.9
[39] 11.1 11.3 11.5 11.7 11.9 12.1 12.3 12.5 12.7 12.9 13.1 13.3 13.5 13.7 13.9 14.1 14.3 14.5
> plot(market$X, market$Y, ylim = range(market$Y, pp))
> matlines(pred.X, pc, lty=c(1,2,2), col='BLUE')
> matlines(pred.X, pp, lty=c(1,3,3), col='RED')
5. $\beta_1$의 검정
앞에서 분산에 대한 것을 구해봤고 이것을 이용하여 t 통계량을 구할 수 있다.
t 검정방법을 이용한 결과값이 크면 클수록 귀무가설을 기각하게 된다.

- $\beta_1$ 검정
> market.lm = lm(Y~X, data = market)
> summary(market.lm)
Call:
lm(formula = Y ~ X, data = market)
Residuals:
Min 1Q Median 3Q Max
-3.600 -1.502 0.813 1.128 4.617
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.2696 3.2123 -0.707 0.499926
X 2.6087 0.3878 6.726 0.000149 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.631 on 8 degrees of freedom
Multiple R-squared: 0.8497, Adjusted R-squared: 0.831
F-statistic: 45.24 on 1 and 8 DF, p-value: 0.0001487여기서 기울기 $\beta_1$의 추정값 $b_1 = 2.6087$, t-value는 2.6087/0.3878=6.726이다.
> # 기각역 및 p-value 구하기
> # 유의수준 0.05 자유도가 13인 기각역
> qt(0.975, 13)
[1] 2.160369
> # 유의확률 p-value
> 2*(1-pt(12.889, 13))
[1] 8.827548e-09
'Data Science > Regression Analysis' 카테고리의 다른 글
| [Regression] 중회귀모형 (0) | 2022.03.31 |
|---|---|
| [Regression] 가중회귀 (0) | 2022.03.31 |
| [Regression] 회귀모형의 평가 분산분석(ANOVA) (0) | 2022.03.11 |
| [Regression] 회귀선의 추정 (0) | 2022.03.09 |
| [Regression] 단순회귀모형 (0) | 2022.03.09 |




댓글